Conservazione del momento angolare: studente su gabello rotante

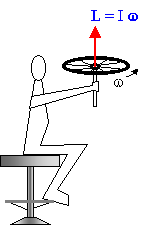
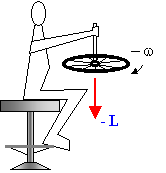
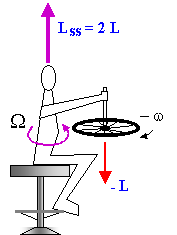
Consideriamo il sistema mostrato in Fig. 1: uno studente seduto su uno sgabello rotante. Inizialmente fermo, sostiene una ruota di bicicletta in moto con velocità angolare w. Lo studente gira l’asse della ruota di 180° come in Fig. 2. Tutto il sistema  (studente sgabello) + ruota prende a ruotare in senso antiorario con velocità angolare W (Fig. 3). Vediamo perché e calcoliamo W.

Dato che il sistema (studente sgabello) + ruota è isolato, cioè:

consegue che:

Calcoliamo il momento angolare del sistema all’istante t, prima che l’asse venga girato, e all’istante t+Dt, dopo che è stato girato:

t	t+ Dt
Fig. 1  Momento angolare ruota                      Momento angolare Sgabello-Studente Momento angolare sistema	Fig. 2 Momento angolare ruota Momento angolare Sgabello-Studente Momento angolare sistema = cost = L Fig. 3

I_SSrappresenta il momento di inerzia del sistema (sgabello studente) + ruota rispetto all'asse verticale dello sgabello.

_______________________

Il fenomeno può essere analizzato suddividendo il sistema (studente sgabello) + ruota nei due sottosistemi:

(studente sgabello) e ruota.

 I due sottosistemi non sono isolati.  Lo studente, nel girare l’asse della ruota,  esercita un momento di forza, t_SS, sulla ruota, e,  a sua volta, per il principio di azione e reazione,  la ruota esercita un momento, t_R,uguale e contrario sullo studente, costringendolo a ruotare. Secondo questa trattazione t_SS et_R sono momenti esterni, cioè prodotti da un sottosistema sull’altro. Nella trattazione precedente le forze esercitate dallo studente sull’asse della ruota sono forze interne che non hanno alcuna influenza sul momento angolare del sistema, perché, secondo l’equazione fondamentale della dinamica dei sistemi,

il momento angolare può cambiare solo per effetto di momenti di forze esterne.