Trovare le probabilita' di uscita per la prima volta del numero 3 nel lancio di un dado al primo, al secondo, all'n-esimo lancio e rappresentarla mediante la distribuzione geometrica
p probabilita' di uscita del numero 3 = 1/6
q probabilita' di non uscita del numero 3 = 5/6
la variabile aleatoria Z sara'
| Z | 1 | 2 | 3 | 4 | ......... | n | |
| f | 1/6 | 5/6·1/6 | (5/6)2·1/6 | (5/6)3·1/6 | ......... | (5/6)n-1·1/6 | |
Cioe'
| Z | 1 | 2 | 3 | 4 | ......... | |
| f | 1/6 | 5/36 | 25/216 | 125/1296 | ......... | |
ed avremo come rappresentazione grafica della distribuzione geometrica
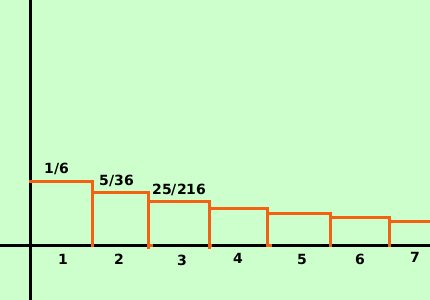
Notiamo anche qui che, siccome l'area di tutti i rettangoli vale 1 (evento certo) e l'area del primo rettangolo vale 1/6 e gli altri valgono meno, l'evento e' sempre piu' probabile che succeda alla prima prova (e' piu' probabile che esca 3 per la prima volta alla prima prova piuttosto che esca 3 per la prima volta al millesimo lancio)
Trovare le probabilita' della prima uscita del numero 1 sulla ruota di Bari alla prima, alla seconda, alla n-esima estrazione e rappresentarla mediante la distribuzione geometrica
Sulla ruota di Bari vengono estratti 5 numeri su 90 possibili (semplifichiamo un poco i calcoli) quindi
p probabilita' di uscita del numero 1 = 5/90 = 1/18
q probabilita' di non uscita del numero 85/90 = 17/18
la variabile aleatoria Z sara'
| Z | 1 | 2 | 3 | ......... | n | |
| f | 1/18 | 17/18·1/18 | (17/18)2·1/18 | ......... | (17/18)n-1·1/18 | |
Cioe'
| Z | 1 | 2 | 3 | 4 | ......... | |
| f | 1/18 | 17/324 | 289/5832 | 4913/104976 | ......... | |
ed avremo come rappresentazione grafica della distribuzione geometrica
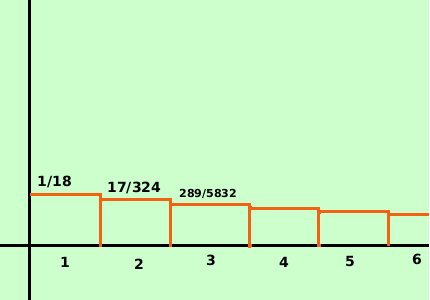
Nessun commento:
Posta un commento