- Si spostano i radicali dalla parte della disequazione dove hanno il segno positivo (nella pagina seguente una giustificazione logica del procedimento)
- Si risolve un sistema le cui disequazioni sono i radicandi posti ciascuno maggiore od uguale a zero e si trova l'intervallo in cui la disequazione e' possibile
- Si procede come per le equazioni irrazionali con opportuni elevamenti a potenza per ridurre i radicali, sino ad ottenere un radicale ed un numero
- Quello che abbiamo ottenuto e' una disequazione elementare del tipo gia' visto: va risolta
- I risultati trovati vanno messi a sistema con l'intervallo in cui e' possibile la disequazione
sposto il secondo radicale dopo il disuguale cambiandolo di segno
imposto il sistema x+2 x+3 ottengo x x 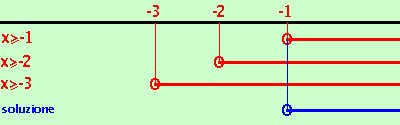 Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto. Abbiamo come soluzione x Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto. Abbiamo come soluzione x Sono tre radicali: elevo a quadrato da una parte e dall'altra
ottengo
Porto i termini fuori radice prima del disuguale e lascio la radice dopo
sommo, moltiplico dentro radice ed ottengo
e' una disequazione irrazionale elementare del secondo tipo che abbiamo visto: risolviamola; devo risolvere i sistemi:
(-x - 4)2 < 4(x2 + 5x + 6) sviluppiamo le equazioni e dopo alcuni calcoli otteniamo: 3x2+12x+8 > 0 La seconda e' sempre verificata (delta minore di zero)  Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto. Essendo un sistema prendo le soluzioni comuni Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto. Essendo un sistema prendo le soluzioni comuni Abbiamo come soluzione x risolviamo il secondo 4(x2 + 5x + 6) Divido la seconda per 4 x2 + 5x + 6 la prima -x -4 < 0 e' verificata per x > -4 la seconda x2 + 5x + 6 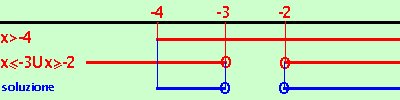 Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto. Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto.Abbiamo come soluzione -4 < x Ora devo mettere assieme le soluzioni dei due sistemi ed ottengo x x 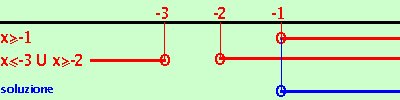 Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto. Riporto su un grafico, evidenziando con una linea marcata i valori che risolvono le disequazioni, i valori dove e' accettabile l'uguale li indico con un cerchietto.Abbiamo come soluzione della disequazione iniziale
|
Nessun commento:
Posta un commento