Formula di Erone

Area del triangolo conoscendone la misura di tre lati
Consideriamo un triangolo qualunque ABC e supponiamo di conoscerne la misura dei tre lati 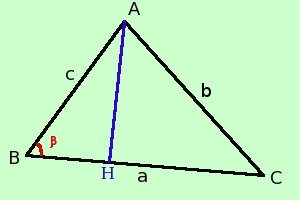in queste condizioni posso ricavare una formula che mi permette di avere l'area del triangolo stesso
Supponiamo di conoscere
AB_ = c
BC_ = a
AC_ = b
con a, b e c numeri noti
Partiamo dalla formula trovata dell'area del triangolo conoscendone due lati e l'angolo compreso

As =

1 2

ac sen

Naturalmente possiamo scegliere un angolo qualunque e i due lati che lo comprendono
Per la formula di duplicazione del seno possiamo scrivere

As =

1 2

2ac sen /2 cos /2

As =	ac sen /2 cos /2

Ora applico le formule di Briggs

As = ac
		(p-a)(p-c) ac		p (p-b) ac

Moltiplico

As = ac
		p(p-a)(p-b)(p-c) a2c2

Ora estraggo a²c² di radice

As =	ac ac
			p(p-a)(p-b)(p-c)

semplifico ed ottengo:

As =
			p(p-a)(p-b)(p-c)